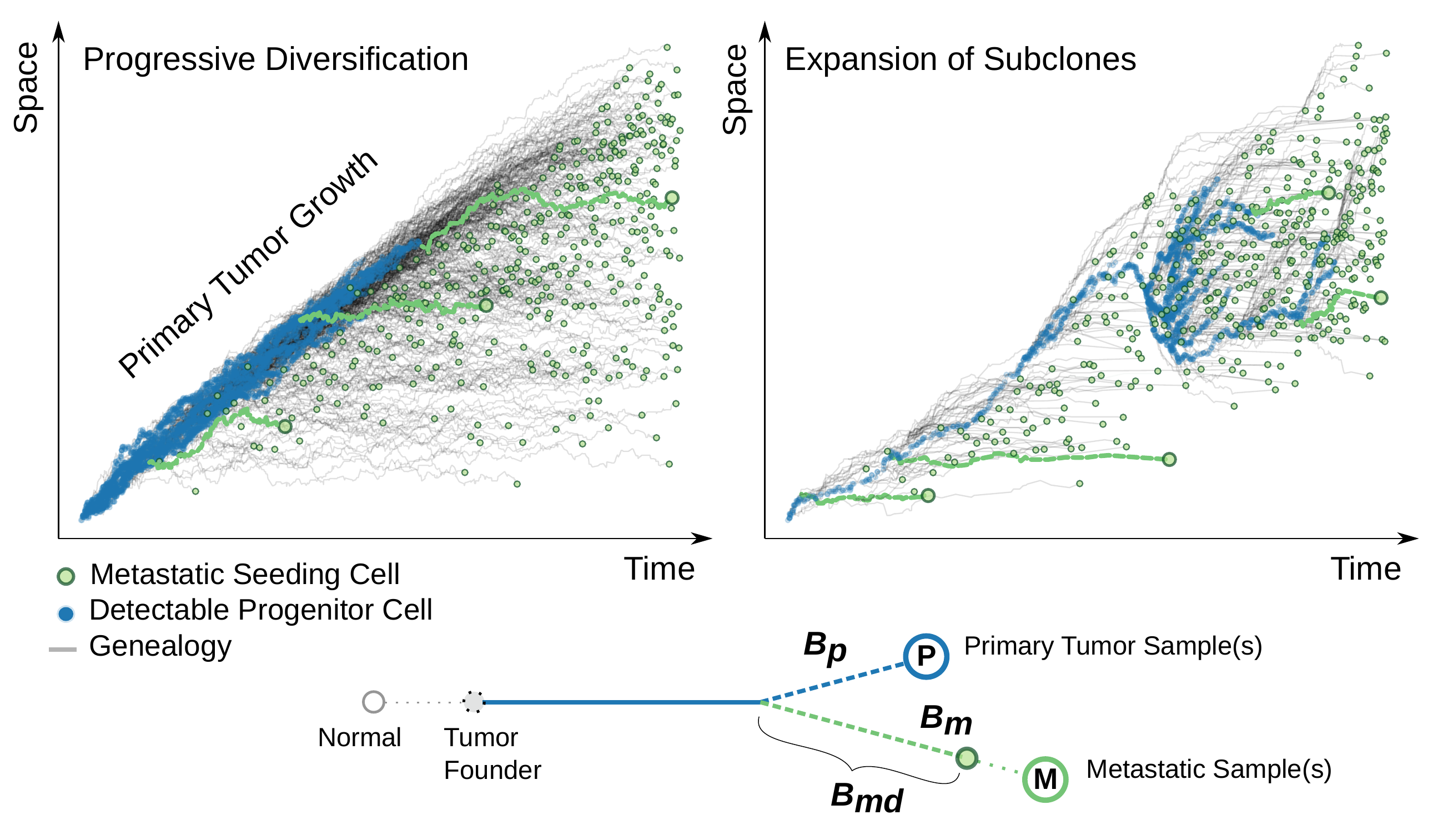
Here we give a snapshot of our recently published paper “Elements and evolutionary determinants of genomic divergence between paired primary and metastatic tumors” in PLoS Computational Biology.

Longitudinal tumor sampling provides us with the opportunity to quantify the between-tumor (stage) genomic divergence. However, it still remains a challenge about how to translate the genomic divergence between paired metastatic and primary tumor samples (M-P divergence) into the natural history of metastatic spread. Given a phylogenetic tree of these tumor samples constructed from NGS data, should we read a small M-P divergence as a sign of “early” metastatic seeding, or evidence of a “late” acquisiton of the metastatic potential? Before answering this clinically relevant question, one needs to characterize what exactly is being captured on the trees of tumor evolution by such divergence.

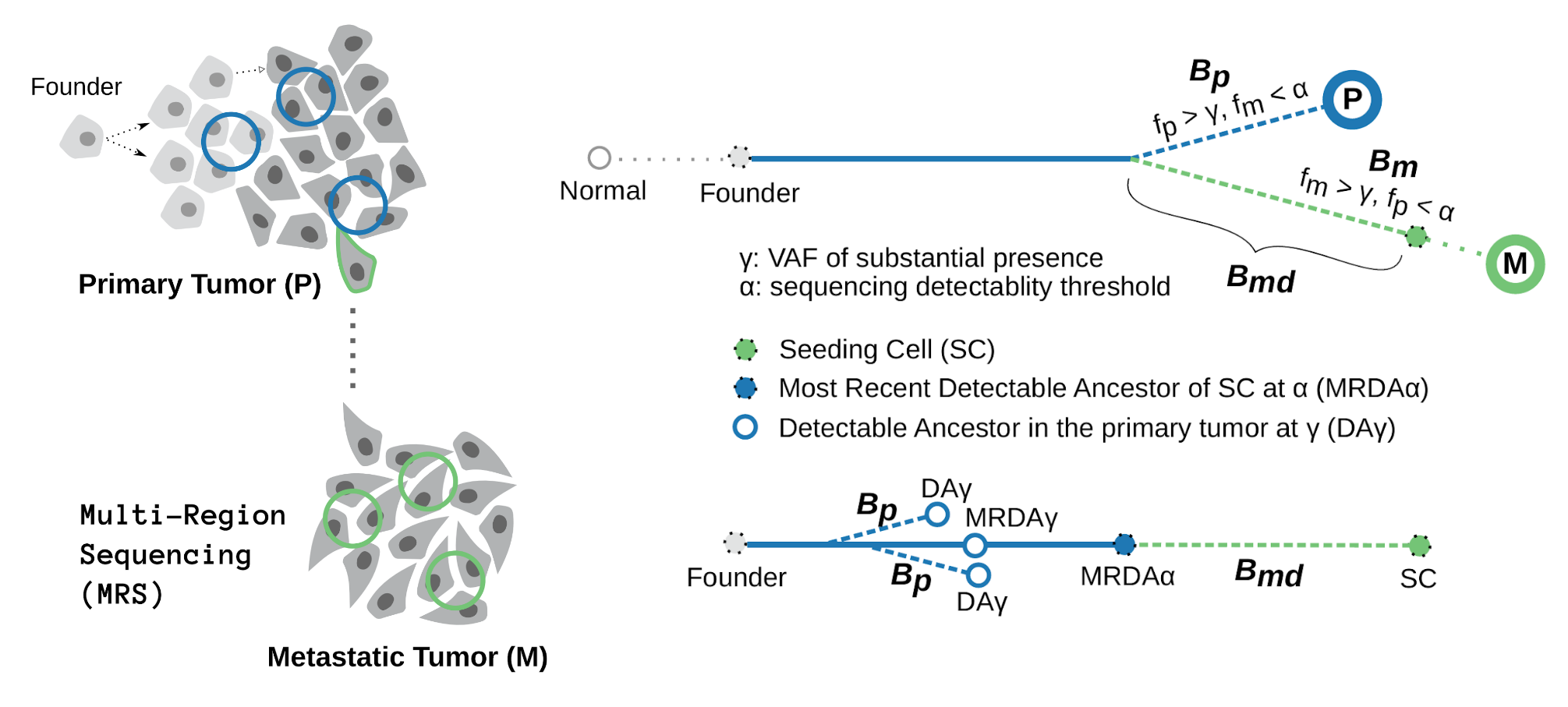
We show that the number of somatic variants of the metastatic seeding cell that are undetectable in the primary tumor sequencing data, i.e., the number of somatic variants specific to the metastatic seeding cell, $B_{md}$, can be characterized as the path of the phylogenetic tree from the last appearing variant of the seeding cell back to the most recent detectable variant (MRDV). In other words, the depth of the MRDV (from the most recent detectable ancestor) in the seeding cell’s lineage characterizes $B_{md}$. Let $k$ represent the total number of somatic variants in the seeding cell, and $\alpha$ to be the sequencing detectablity threshold, we have

\begin{equation} B^k_{md} = k - V_{MRDA}(k, \alpha) \end{equation}

Further, we find that the expected length of this path is principally determined by the decay in detectability of the variants along the seeding cell’s lineage; and thus, exhibits a significant dependence on the underlying tumor growth dynamics.

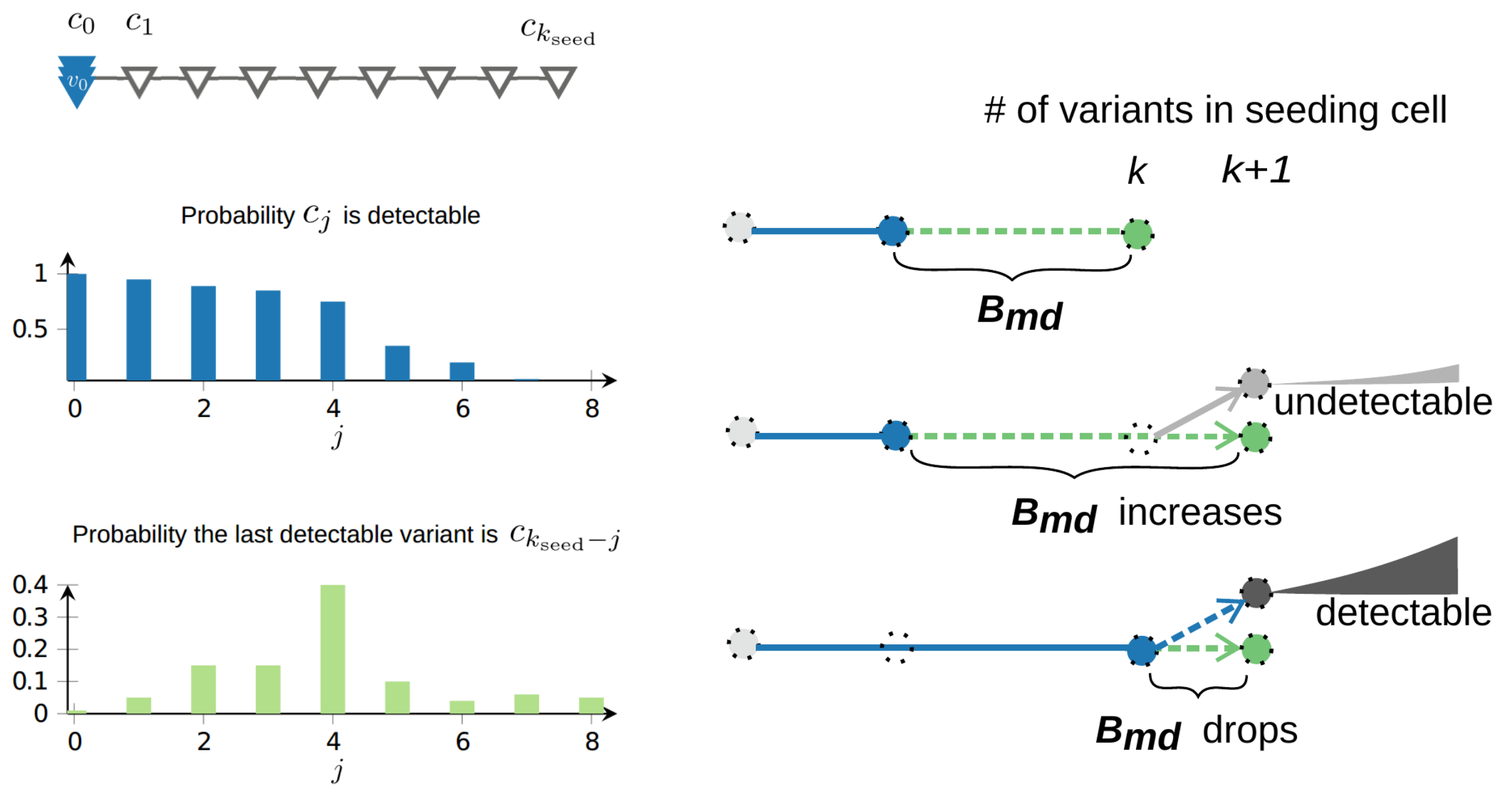
Let $c$ be a seeding cell of a secondary tumor (as opposed to the primary tumor) and also let \begin{equation} C = (c_0, c_1, . . . , c_{k_{seed}}) \end{equation} be its associated set of variants, indexed according to the order of appearance as the primary tumor expands. Let $d_{c_j}$ denote the probability variant $c_j$ ends up being detectable in the primary tumor. We found that under the infinite allele model, the probability that $B_m^k$, the number of variants specific to the metastatic seeding cell (with $k$ somatic variants in total) take value $i$ can be expressed in a surprisingly simple form in terms of $d_{c_j}$:

\begin{equation} Pr[B_m^k = i] = d_{c_{k-i}} - d_{c_{k-i+1}}. \end{equation}

As a result, despite the accumulation of somatic variants in the seeding cell as the primary tumor expands, dissemination from a late detectable subclone leads to an abrupt drop in $B_{md}$. Such effect is unavoidable when dissemination capability is positively associated with fitness advantage, however our math modeling indicates that the expected drop in $B_{md}$ remains significant even when seeding happens uniformly at random from all living cells.

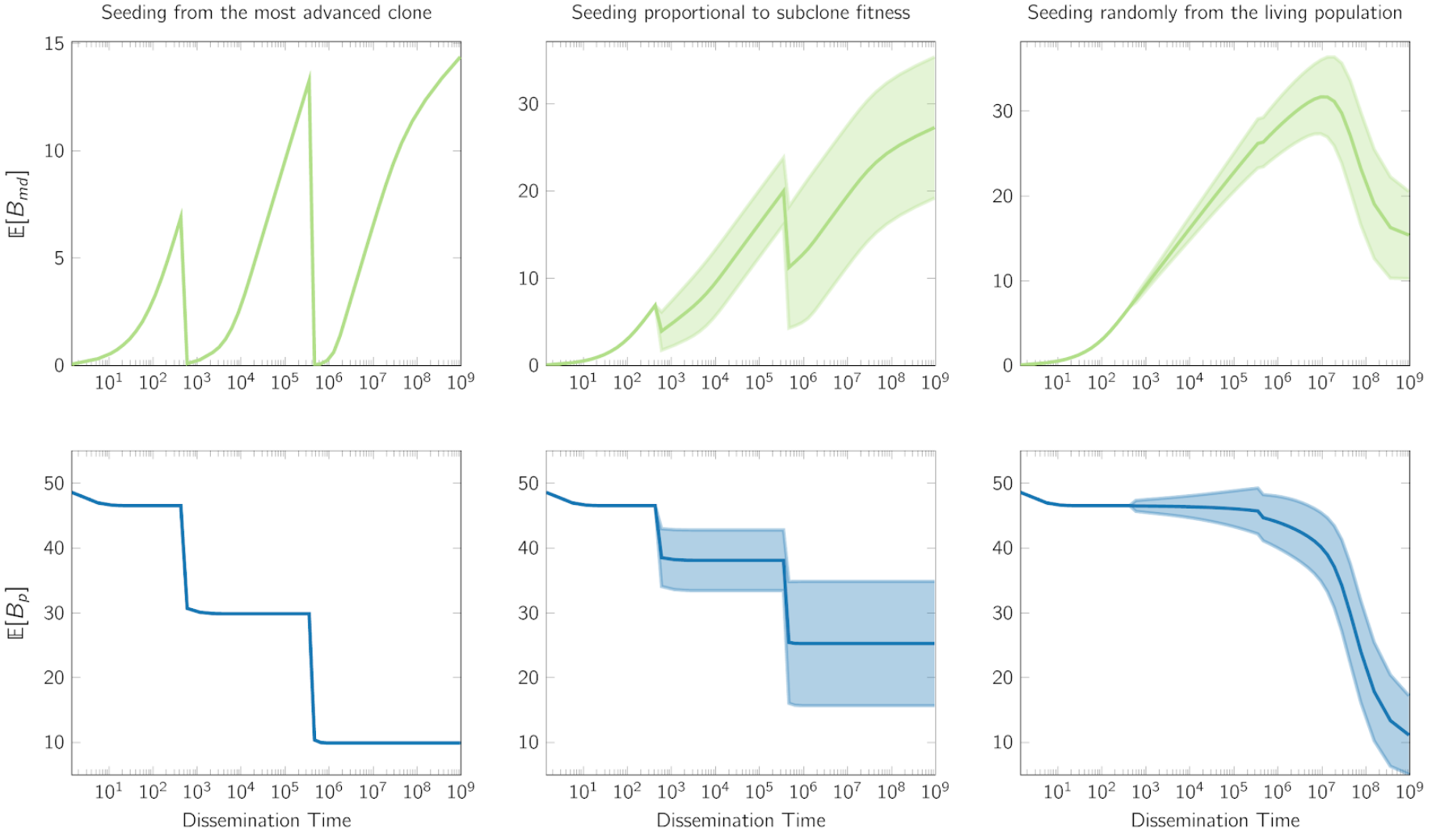
Finally, our spatial modeling verifies that the growth mode governs M-P divergence dependency on seeding time. The non-monotonic pattern revealed here has implications for the accurate translation of the genomic measurement. We hope to pave the way towards bridging the measurable between-tumor heterogeneity with analytical modeling and interpretability.

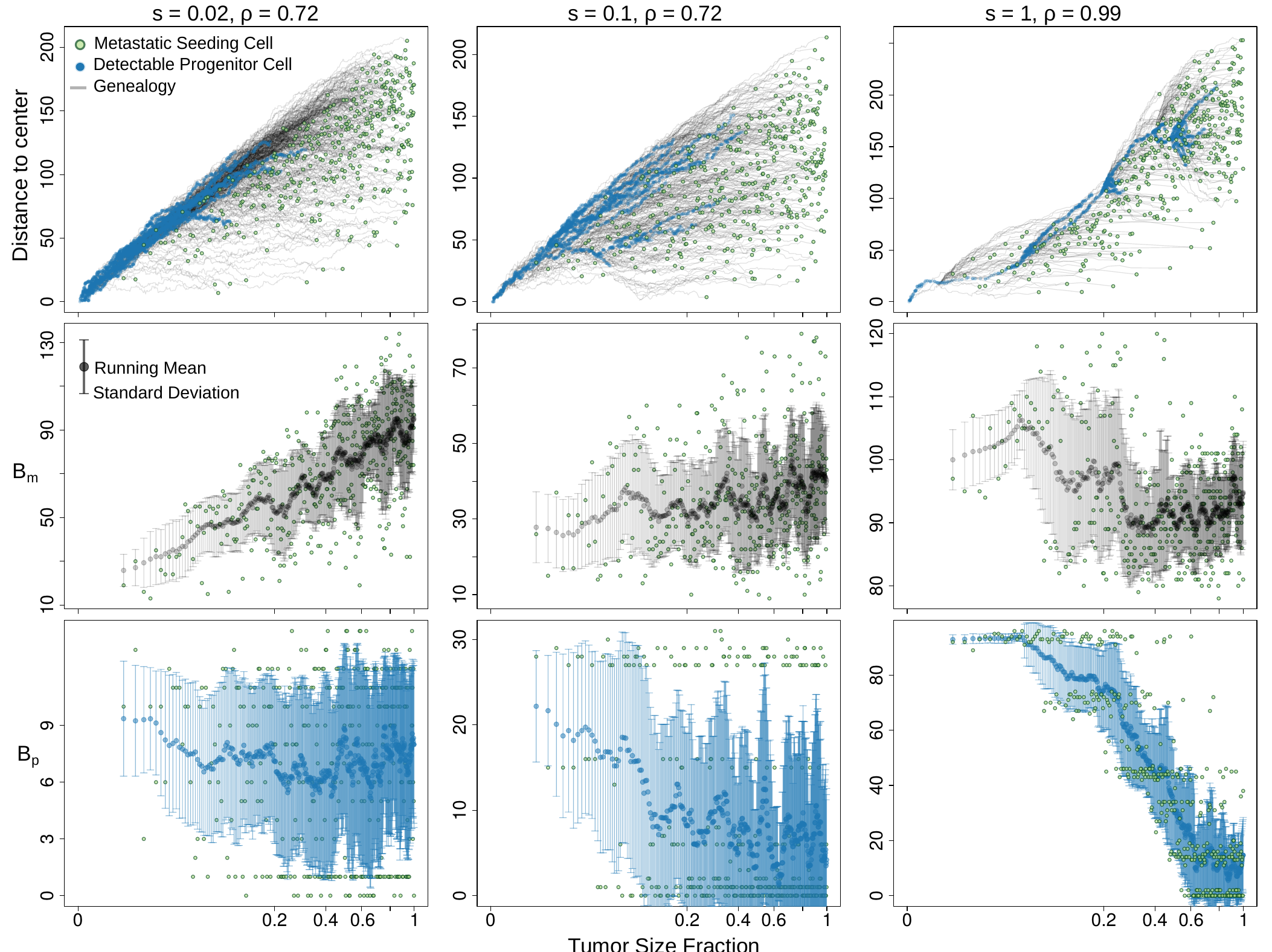
We left the modeling of primary specific variants, $B_p$, as a homework for you to think. Hint: $B_p$ is the total branch length of the genealogies of detectable ancestors at a frequency above $\gamma$ (the variant allele frequency threshold suggesting the substantial presence), after subtracting the branch between the founder and the MRDA (at a frequency above $\gamma$) of the seeding cell. We hope that you enjoy this exercise, and the answer is here.